Affiliate links on Android Authority may earn us a commission. Learn more.
The great audio myth: why you don’t need that 32-bit DAC

As you have probably noticed, there’s a new trend in the smartphone industry of including “studio quality” audio chips inside modern flagship smartphones. While a 32-bit DAC (digital to analog converter) with 192kHz audio support certainly looks good on the spec sheet, there simply isn’t any benefit to pushing up the size of our audio collections.
I’m here to explain why this bit depth and sample rate boasting is just another instance of the audio industry taking advantage of the lack of consumer and even audiophile knowledge on the subject. Don your nerd caps, we’re going into some seriously technical points to explain the ins and outs of pro audio. And hopefully I’ll also prove to you why you should ignore most of the marketing hype.
Do you hear that?
Before we dive on in, this first segment offers some required background information on the two main concepts of digital audio, bit-depth and sample rate.
Sample rate refers to how often we are going to capture or reproduce amplitude information about a signal. Essentially, we chop up a waveform into lots of little parts to learn more about it at a specific point in time. The Nyquist Theorem states that the highest possible frequency that can be captured or reproduced is exactly half that of the sample rate. This is quite simple to imagine, as we need the amplitudes for the top and bottom of the waveform (which would require two samples) in order to accurately know its frequency.
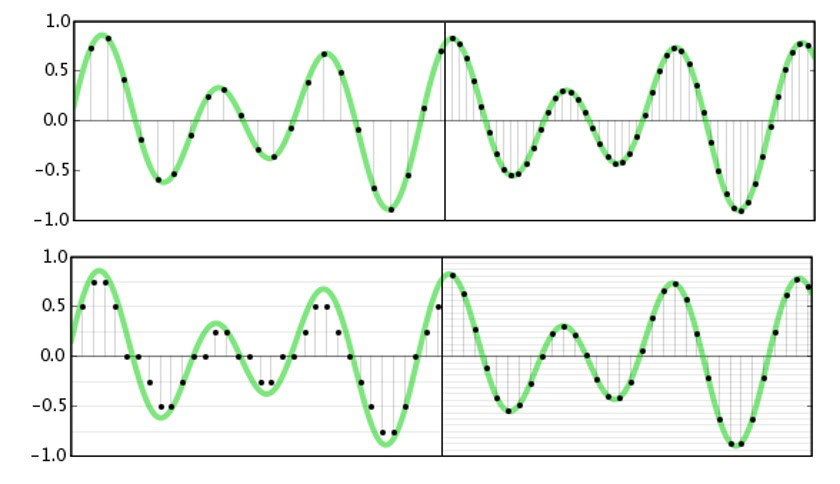
For audio, we are only concerned with what we can hear and the vast majority of people’s hearing tails off just before 20kHz. Now that we know about the Nyquist Theorem, we can understand why 44.1kHz and 48kHz are common sampling frequencies, as they are just over twice the maximum frequency we can hear. The adoption of studio quality 96kHz and 192kHz standards has nothing to do with capturing higher frequency data, that would be pointless. But we’ll dive into more of that in a minute.
As we are looking at amplitudes over time, the bit-depth simply refers to the resolution or number of points available in order to store this amplitude data. For example, 8-bits offers us 256 different points to round to, 16-bit results in 65,534 points, and 32-bits worth of data gives us 4,294,967,294 data points. Although obviously, this greatly increases the size of any files.
| Stereo PCM file size per minute (approx. uncompressed) | 48kHz | 96kHz | 192kHz |
|---|---|---|---|
| Stereo PCM file size per minute (approx. uncompressed) 16-bit | 48kHz 11.5MB | 96kHz 23.0MB | 192kHz 46.0MB |
| Stereo PCM file size per minute (approx. uncompressed) 24-bit | 48kHz 17.3MB | 96kHz 34.6MB | 192kHz 69.1MB |
| Stereo PCM file size per minute (approx. uncompressed) 32-bit | 48kHz 23.0MB | 96kHz 46MB | 192kHz 92.2MB |
It might be easy to immediately think about bit-depth in terms of amplitude accuracy, but the more important concepts to understand here are that of noise and distortion. With a very low resolution, we will likely miss out chunks of lower amplitude information or cut off the tops of waveforms, which introduces inaccuracy and distortion (quantisation errors). Interestingly, this will often sound like noise if you were to play back a low resolution file, because we have effectively increased the size of the smallest possible signal that can be captured and reproduced. This is exactly the same as adding a source of noise to our waveform. In other words, lowering the bit-depth also decreases the noise floor. It might also help to think of this in terms of a binary sample, where the least significant bit represent the noise floor.
Therefore, a higher bit-depth gives us a greater noise floor, but there is a finite limit to how practical this is in the real world. Unfortunately, there is background noise everywhere, and I don’t mean the bus going past on the street. From cables to your headphones, the transistors in an amplifier, and even the ears inside your head, the maximum signal to noise ratio in the real world is around 124dB, which works out to roughly 21-bits worth of data.
Jargon Buster:
DAC- A digital-to-analog converter takes digital audio data and transforms it into an analog signal to send to headphones or speakers.
Sample Rate- Measured in Hertz (Hz), this is the number of digital data samples captured each and every second.
SNR- Signal-to-noise ratio is the difference between the desired signal and the background system noise. In a digital system this is linked directly to the bit-depth.
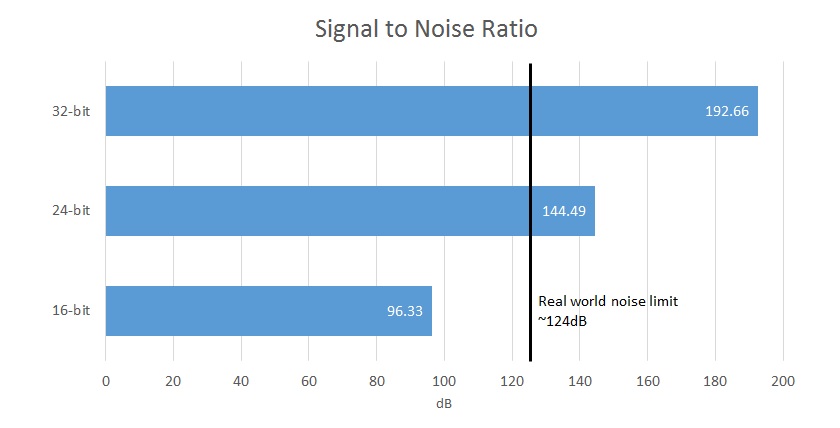
For comparison, 16-bits of capture offers a signal to noise ratio (the difference between the signal and background noise) of 96.33dB, while 24-bit offers 144.49dB, which exceeds the limits of hardware capture and human perception. So your 32-bit DAC is actually only ever going to be able to output at most 21-bits of useful data and the other bits will be masked by circuit noise. In reality though, most moderately priced pieces of equipment top out with an SNR of 100 to 110dB, as most other circuit elements will introduce their own noise. Clearly then, 32-bit files already seem rather redundant.
Now that we have the basics of digital audio understood, let’s move on to some of the more technical points.
[related_videos title=”Phones boasting top-notch audio:” align=”center” type=”custom” videos=”654322,663697,661117,596131″]
Stairway to Heaven
Most of the issues surrounding the understanding and misconception of audio is related to the way in which educational resources and companies attempt to explain the benefits using visual cues. You have probably all seen audio represented as a series of stair steps for bit-depth and rectangular looking lines for the sample rate. This certainly doesn’t look very good when you compare it to a smooth looking analog waveform, so it’s easy to trot out finer looking, “smoother” staircases to represent a more accurate output waveform.
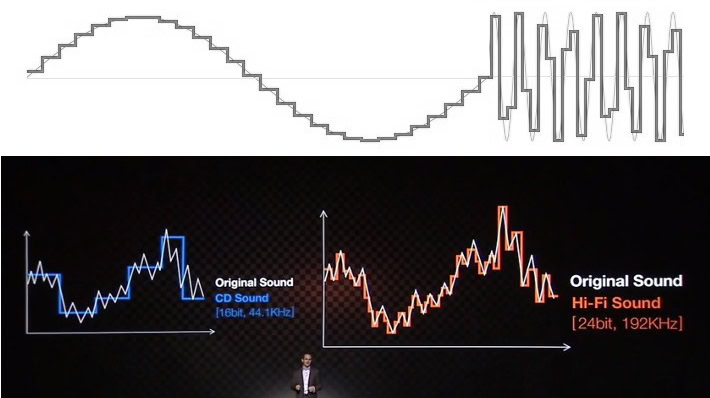
However, this visual representation misrepresents how audio works. Although it may looks messy, mathematically the data below the Nyquist frequency, that’s half of the sampling rate, has been captured perfectly and can be reproduced perfectly. Picture this, even at the Nyquist frequency, which may often be represented as a square wave rather than a smooth sine wave, we have accurate data for the amplitude at a specific point in time, which is all we need. We humans are often mistakenly looking at the space in-between the samples, but a digital system does not operate in the same way.
Bit-depth is often linked to accuracy, but really it defines the system's noise performance. In other words, the smallest detectable or reproducible signal.
When it comes to playback, this can get a little trickier, because of the easy to understand concept of “zero-order hold” DACs, which will simply switch between values at a set sample rate, producing a stair stepped result. This isn’t actually a fair representation of how audio DACs work, but while we are here we can use this example to prove that you shouldn’t be concerned about those stairs anyway.
An important fact to note is that all waveforms can be expressed as the sum of multiple sine waves, a fundamental frequency and additional components at harmonic multiples. A triangle wave (or a stair step) consists of odd harmonics at diminishing amplitudes. So, if we have lots of very small steps occurring at our sample rate, we can say that there is some extra harmonic content added, but it occurs at double our audible (Nyquist) frequency and probably a few harmonics beyond that, so we won’t be able to hear them anyway. Furthermore, this would be quite simple to filter out using a few components.
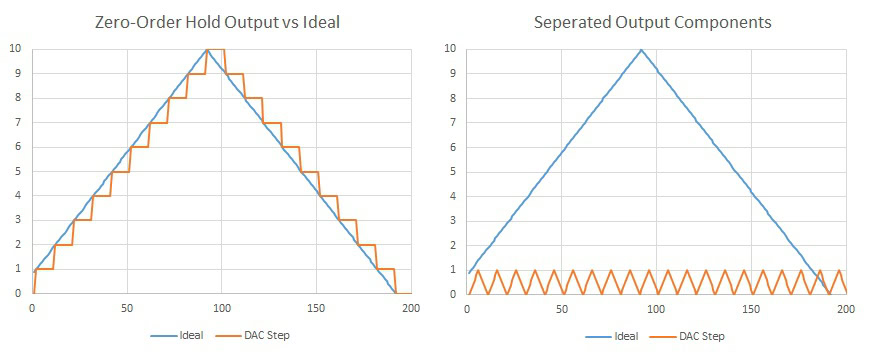
If this is true, we should be able to observe this with a quick experiment. Let’s take an output straight from a basic zero-order hold DAC and also feed the signal through a very simple 2nd order low pass filter set at half our sample rate. I’ve actually only used a 6-bit signal here, just so that we can actually see the output on an oscilloscope. A 16-bit or 24-bit audio file would have far less noise on the signal both before and after filtering.

And as if by magic, the stair stepping almost completely disappeared and the output is “smoothed out”, just by using a low-pass filter that doesn’t interfere with our sine wave output. In reality, all we have done is filtered out parts of the signal that you wouldn’t have heard anyway. That’s really not a bad result for an extra four components that are basically free (two capacitors and two resistors cost less than 5 pence), but there are actually more sophisticated techniques that we can use to reduce this noise even further. Better yet, these are included as standard in most good quality DACs.
Dealing with a more realistic example, any DAC for use with audio will also feature an interpolation filter, also known as up-sampling. Interpolation is quite simply a way of calculating intermediate points in between two samples, so your DAC is actually doing a lot of this “smoothing” on its own, and much more so than doubling or quadrupling the sample rate would. Better yet, it doesn’t take up any extra file space.
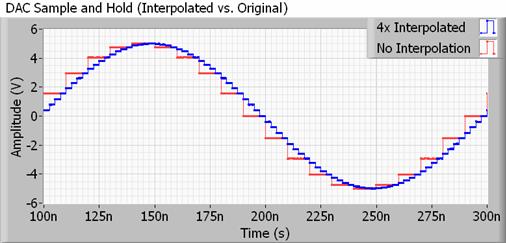
The methods to do this can be quite complex, but essentially your DAC is changing its output value much more often than the sample frequency of your audio file would suggest. This pushes the inaudible stair step harmonics far outside of the sampling frequency, allowing for the use of slower, more readily achievable filters that have less ripple, therefore preserving the bits that we actually want to hear.
If you’re curious as to why we want to remove this content that we can’t hear, the simple reason is that reproducing this extra data further down the signal chain, say in an amplifier, would waste energy. Furthermore depending on other components in the system, this higher frequency “ultra-sonic” content might actually lead to higher amounts of intermodulation distortion in limited bandwidth components. Therefore, your 192 kHz file would probably be causing more harm than good, if there was actually any ultra-sonic content contains within those files.
If any more proof were needed, I’ll also show an output from a high quality DAC using the Circus Logic CS4272 (pictured at the top). The CS4272 features an interpolation section and steep built in output filter. All we are doing for this test is using a micro-controller to feed the DAC two 16-bit high and low samples at 48kHz, giving us the maximum possible output waveform at 24kHz. There are no other filtering components used, this output comes straight from the DAC.
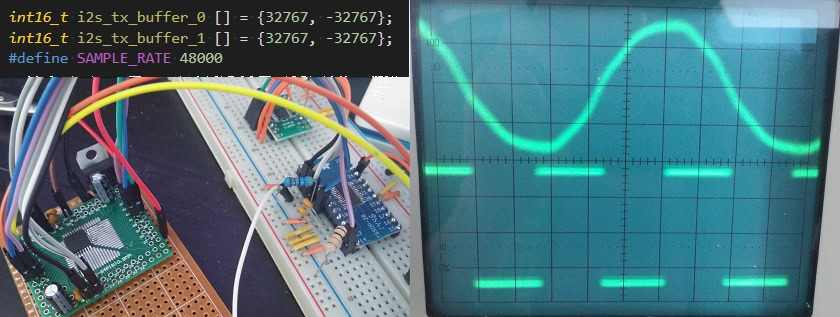
Note how the output sine wave (top) is exactly half the speed of the frequency clock (bottom). There are no noticeable stair steps and this very high frequency waveform looks almost like a perfect sine wave, not a blocky looking square wave that the marketing material or even a casual glimpse at the output data would suggest. This shows that even with only two samples, the Nyquist theory works perfectly in practise and we can recreate a pure sine wave, absent of any additional harmonic content, without a huge bit-depth or sample rate.
The truth about 32-bit and 192 kHz
As with most things, there is some truth concealed behind all the jargon and 32-bit, 192 kHz audio is something that has a practical use, just not in the palm of your hand. These digital attributes actually come in handy when you’re in a studio environment, hence the claims to bring “studio quality audio to mobile”, but these rules simply don’t apply when you want to put the finished track into your pocket.
First off, let’s start with sample rate. One often touted benefit of higher resolution audio is the retention of ultra-sonic data that you can’t hear but impacts the music. Rubbish, most instruments fall off well before our hearing’s frequency limits, microphone used to capture a space roll off at most around 20kHz, and your headphones that you’re using certainly won’t extend that far either. Even if they could, your ears simply can’t detect it.
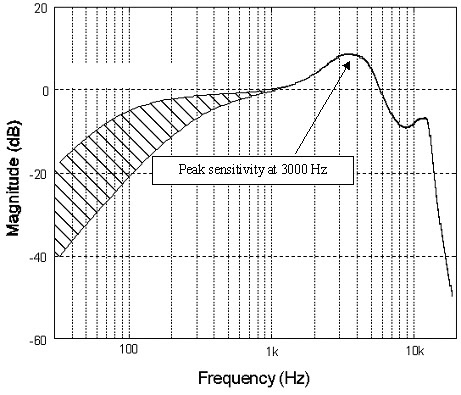
However, 192 kHz sampling is quite useful at reducing noise (that key word yet again) when sampling data, allows for simpler construction of essential input filters, and is also important for high speed digital effect. Oversampling above the audible spectrum allows us to average out the signal to push down the noise floor. You’ll find that most good ADCs (analog to digital converters) these days come with built in 64-bit over-sampling or more.
Every ADC also needs to remove frequencies above its Nyquist limit, or you will end up with horrible sounding aliasing as higher frequencies are “folded down” into the audible spectrum. Having a larger gap between our 20 kHz filter corner frequency and the maximum sample rate is more accommodating to real world filters which simply can’t be as steep and stable as the theoretical filters required. This same is true at the DAC end, but as we discussed intermodulation can very effectively push this noise up to higher frequencies for easier filtering.
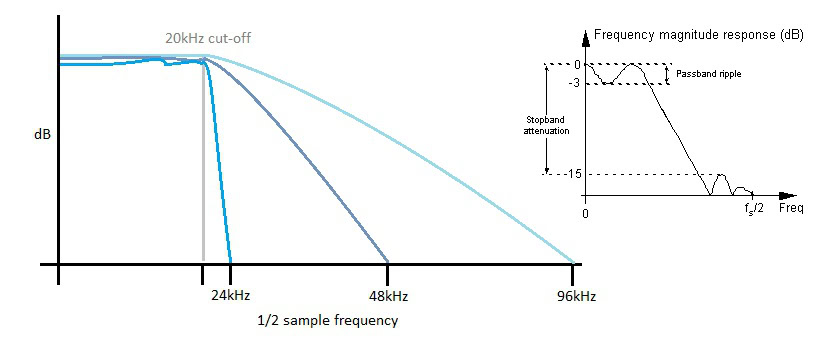
In the digital domain, similar rules apply for filters that are often used in the studio mixing process. Higher sample rates allow for steeper, faster acting filters that require additional data in order to function properly. None of this is required when it comes to playback and DACs, as we are only interesting in what you can actually hear.
Moving on to 32-bit, anyone who has ever attempted to code any remotely complex mathematics will understand the importance of bit depth, both with integer and floating point data. As we’ve discussed, the more bits the less noise and this becomes more important when we start dividing or subtracting signals in the digital domain because of rounding errors and to avoid clipping errors when multiplying or adding.
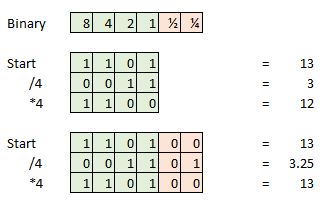
Here’s an example, say we take a 4-bit sample and our current sample is 13, which is 1101 in binary. Now attempt to divide that by four and we are left with 0011, or simply 3. We have lost the extra 0.25 and this will represent an error if we attempted to do additional math or turn our signal back into an analog wave form.
These rounding errors manifest as very small amounts of distortion or noise, which can accumulate over a large number of mathematical functions. However, if we extended this 4-bit sample with additional bits of information to use as a faction or decimal point then we can continue to divide, add and multiple for a lot longer thanks to the extra data points. So in the real world, sampling at 16 or 24 bit and then converting this data into a 32-bit format for processing again helps to save on noise and distortion. As we’ve already stated, 32-bits is an awful lot of points of accuracy.
Now, what is equally important to recognise is that we don’t need this extra headroom when we come back into the analog domain. As we have already discussed, around 20-bits of data (-120dB of noise) the absolute maximum that can possibly detect, so we can convert back to a more reasonable file size without affecting audio quality, despite the fact that “audiophiles” are probably lamenting this lost data.
However, we will inevitably introduce some rounding errors when moving to a lower bit depth so there will always be some very small amount of extra distortion as these errors don’t always occur randomly. While this isn’t a problem with 24-bit audio as it already extends well beyond the analog noise floor, a technique called “dithering” neatly solves this problem for 16-bit files.
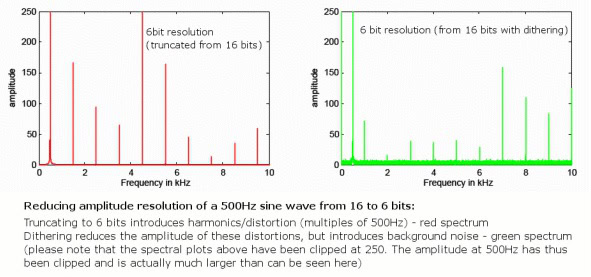
This is done by randomising the least significant bit of the audio sample, eliminating distortion errors but introducing some very quiet random background noise that is spread across frequencies. Although introducing noise might see counter intuitive, this actually reduces the amount of audible distortion because of the randomness. Furthermore, using special noise-shaped dithering patterns that abuse the frequency response of the human ear, 16-bit dithered audio can actually retain a perceived noise floor very close to 120dB, right at the limits of our perception.

Simply put, let the studios clog up their hard drives with this high resolution content, we simply don’t need all of that superfluous data when it comes to high quality playback.
Wrap Up
If you are still with me, don’t construe this article as a complete dismissal of the efforts to improve smartphone audio components. Although the number touting may be useless, higher quality components and better circuit design is still an excellent development in the mobile market, we just need to make sure manufacturers focus their attention on the right things. The 32-bit DAC in the LG V10, for instance, sounds amazing, but you don’t need to bother with huge audio file sizes to take advantage of it.

The ability to drive low impedance headphones, preserve a low noise floor from the DAC to the jack, and offer minimal distortion are much more important characteristics for smartphone audio than the theoretically supported bit-depth or sample rate, and we’ll hopefully be able to dive into these points in more detail in the future.